A análise de complexidade de algoritmos é uma prática essencial na ciência da computação, projetada para avaliar o desempenho desses algoritmos em relação aos recursos computacionais. Tempo de execução e espaço de memória são critérios cruciais considerados nesse processo, visando compreender como o desempenho varia conforme o tamanho da entrada, indicando como o tempo de execução ou uso de espaço se comporta diante do crescimento dos dados de entrada.
A Importância da Análise de Complexidade
A análise de complexidade não é apenas uma formalidade acadêmica, mas sim uma ferramenta indispensável na engenharia de software. Ela proporciona insights valiosos para aprimorar algoritmos, tornando-os mais eficientes e capazes de lidar com conjuntos de dados cada vez maiores. Ao analisar os aspectos de processamento e espaço, garantimos não apenas um desempenho otimizado em condições ideais, mas também a resiliência do algoritmo diante do crescimento das entradas.
Casos de Análise: Melhor Caso, Caso Médio, Pior Caso
A análise de complexidade considera três cenários distintos: melhor caso, caso médio e pior caso. O melhor caso reflete a situação otimista, onde o algoritmo alcança sua eficiência máxima. O caso médio é uma média ponderada das execuções sob diferentes condições. O pior caso representa o cenário mais desafiador, revelando a performance menos eficiente do algoritmo.
Notação Big O e Além: Entendendo a Eficiência
A notação Big O (O) é uma ferramenta crucial na análise de complexidade, fornecendo uma linguagem padronizada para descrever como o tempo de execução ou espaço de memória aumenta em relação ao tamanho da entrada (denominado “n”). No entanto, a análise de complexidade vai além da notação Big O, considerando outros fatores como constantes multiplicativas, coeficientes dominantes e análise assintótica detalhada.
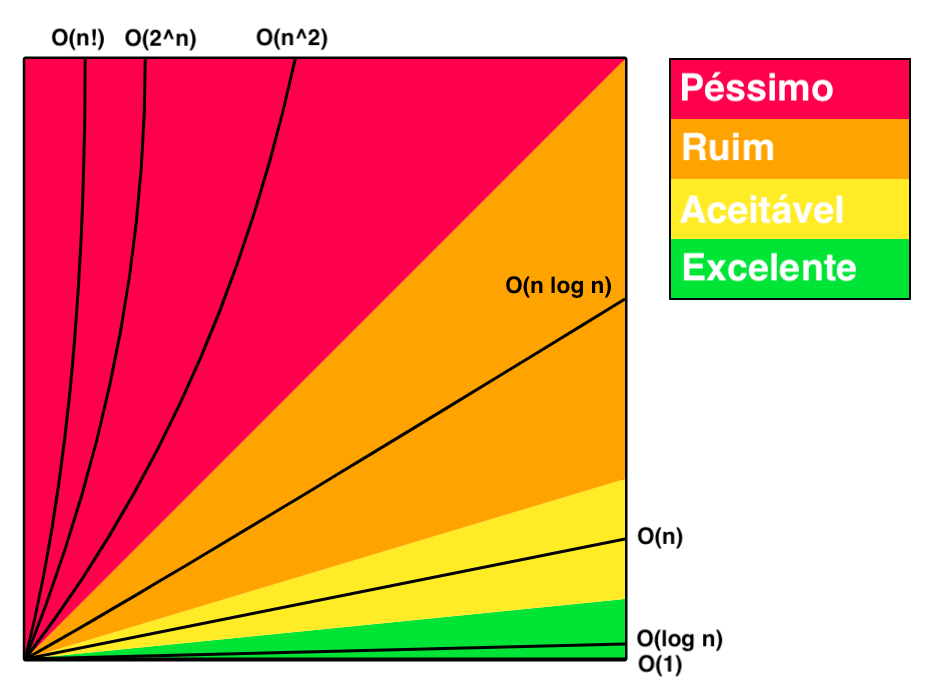 Imagem retirada de https://dicionariotec.com/posts/notacao-do-big-o
Imagem retirada de https://dicionariotec.com/posts/notacao-do-big-o
Classes de Complexidade e Suas Definições
Além da notação Big O, existem diversas classes de complexidade que oferecem uma visão mais granular do desempenho dos algoritmos em diferentes cenários:
- O(1) Constante: Tempo ou espaço de execução constante, independente do tamanho da entrada.
- O(log n) Logarítmica: Crescimento logarítmico, comum em algoritmos eficientes de divisão e conquista.
- O(n) Linear: Crescimento proporcional ao tamanho da entrada, típico em algoritmos de varredura única.
- O(n log n) Linearítmica: Comum em algoritmos eficientes de ordenação, como o merge sort.
- O(n^2) Quadrática: Crescimento quadrático em relação ao tamanho da entrada, presente em algoritmos de ordenação ingênuos.
- O(2^n) Exponencial: Crescimento exponencial, geralmente encontrado em algoritmos recursivos ineficientes.
- O(n!) Fatorial: Crescimento fatorial, associado a algoritmos extremamente ineficientes, como permutações completas.
Conclusão: Moldando a Eficiência dos Algoritmos
A análise de complexidade é uma jornada essencial para desenvolvedores, pois fornece as ferramentas necessárias para criar algoritmos eficientes. Ao entender não apenas a notação Big O, mas também outras nuances da análise de complexidade, os desenvolvedores podem fazer escolhas mais informadas e eficazes. Buscar algoritmos com complexidades menores é uma prática que não apenas otimiza o presente, mas prepara o terreno para os desafios computacionais futuros. Portanto, adentre no universo da análise de complexidade, explore suas nuances e transforme seus algoritmos em verdadeiras joias da computação.